2. Plotting fits

library(mobster)
library(tidyr)
library(dplyr)

This vignette describes the plotting functions available in mobster. As an example, we use one of the available datasets where we annotate some random mutations as drivers.

# Example data where we have 3 events as drivers
example_data = Clusters(mobster::fit_example$best) %>% dplyr::select(VAF)

# Drivers annotation (we selected this entries to have nice plots)
drivers_rows = c(2239, 3246, 3800)

example_data$is_driver = FALSE
example_data$driver_label = NA

example_data$is_driver[drivers_rows] = TRUE
example_data$driver_label[drivers_rows] = c("DR1", "DR2", "DR3")

# Fit and print the data
fit = mobster_fit(example_data, auto_setup = 'FAST')
#>  [ MOBSTER fit ] 
#> 
#> ✔ Loaded input data, n = 5000.
#> ❯ n = 5000. Mixture with k = 1,2 Beta(s). Pareto tail: TRUE and FALSE. Output
#> clusters with π > 0.02 and n > 10.
#> ! mobster automatic setup FAST for the analysis.
#> ❯ Scoring (without parallel) 2 x 2 x 2 = 8 models by reICL.
#> ℹ MOBSTER fits completed in 8.6s.
#> ── [ MOBSTER ] My MOBSTER model n = 5000 with k = 1 Beta(s) and a tail ─────────
#> ● Clusters: π = 54% [C1] and 46% [Tail], with π > 0.
#> ● Tail [n = 2227, 46%] with alpha = 1.1.
#> ● Beta C1 [n = 2773, 54%] with mean = 0.48.
#> ℹ Score(s): NLL = -5332.99; ICL = -10291.86 (-10614.88), H = 323.01 (0). Fit
#> converged by MM in 11 steps.
#> ℹ The fit object model contains also drivers annotated.
#> # A tibble: 3 × 4
#>      VAF is_driver driver_label cluster
#>    <dbl> <lgl>     <chr>        <chr>  
#> 1 0.448  TRUE      DR1          C1     
#> 2 0.159  TRUE      DR2          Tail   
#> 3 0.0629 TRUE      DR3          Tail

best_fit = fit$best
print(best_fit)
#> ── [ MOBSTER ] My MOBSTER model n = 5000 with k = 1 Beta(s) and a tail ─────────
#> ● Clusters: π = 54% [C1] and 46% [Tail], with π > 0.
#> ● Tail [n = 2227, 46%] with alpha = 1.1.
#> ● Beta C1 [n = 2773, 54%] with mean = 0.48.
#> ℹ Score(s): NLL = -5332.99; ICL = -10291.86 (-10614.88), H = 323.01 (0). Fit
#> converged by MM in 11 steps.
#> ℹ The fit object model contains also drivers annotated.
#> # A tibble: 3 × 4
#>      VAF is_driver driver_label cluster
#>    <dbl> <lgl>     <chr>        <chr>  
#> 1 0.448  TRUE      DR1          C1     
#> 2 0.159  TRUE      DR2          Tail   
#> 3 0.0629 TRUE      DR3          Tail

Model plots

The plot reports some fit statistics, and shows the annotated drivers if any.

plot(best_fit)
#> Warning: Using `size` aesthetic for lines was deprecated in ggplot2 3.4.0.
#> ℹ Please use `linewidth` instead.
#> ℹ The deprecated feature was likely used in the mobster package.
#>   Please report the issue at <https://github.com/caravagnalab/mobster/issues>.
#> This warning is displayed once every 8 hours.
#> Call `lifecycle::last_lifecycle_warnings()` to see where this warning was
#> generated.
#> Warning: The `<scale>` argument of `guides()` cannot be `FALSE`. Use "none" instead as
#> of ggplot2 3.3.4.
#> ℹ The deprecated feature was likely used in the mobster package.
#>   Please report the issue at <https://github.com/caravagnalab/mobster/issues>.
#> This warning is displayed once every 8 hours.
#> Call `lifecycle::last_lifecycle_warnings()` to see where this warning was
#> generated.
#> Warning: The dot-dot notation (`..count..`) was deprecated in ggplot2 3.4.0.
#> ℹ Please use `after_stat(count)` instead.
#> ℹ The deprecated feature was likely used in the mobster package.
#>   Please report the issue at <https://github.com/caravagnalab/mobster/issues>.
#> This warning is displayed once every 8 hours.
#> Call `lifecycle::last_lifecycle_warnings()` to see where this warning was
#> generated.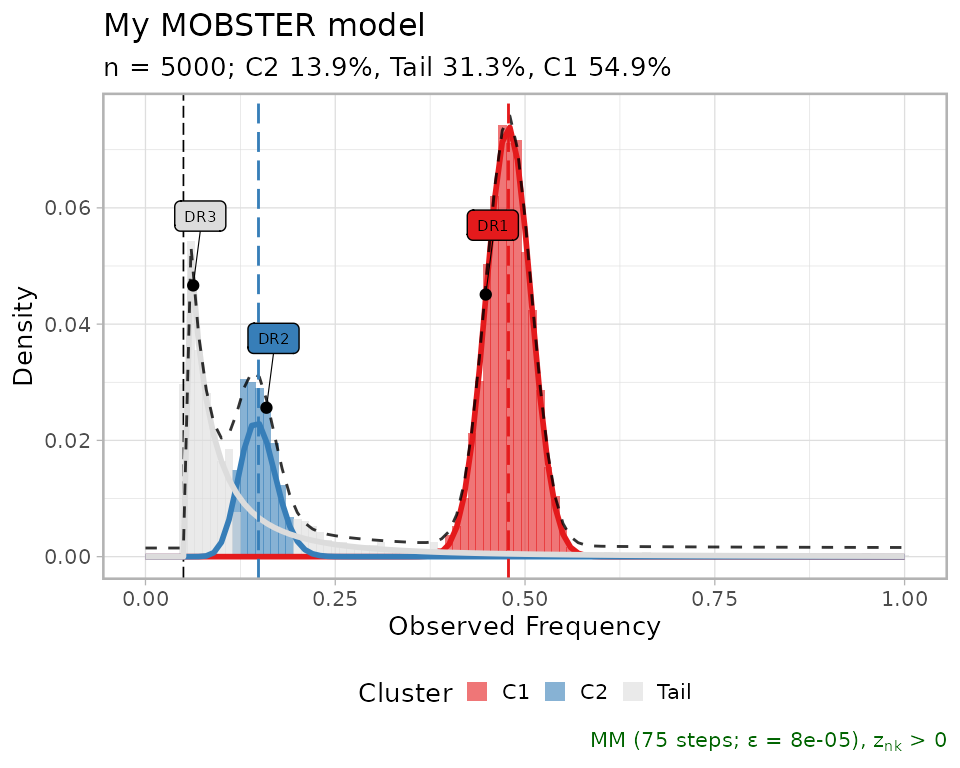

One can hide the drivers setting is_driver to FALSE.

copy_best_fit = best_fit 
copy_best_fit$data$is_driver = FALSE 

plot(copy_best_fit)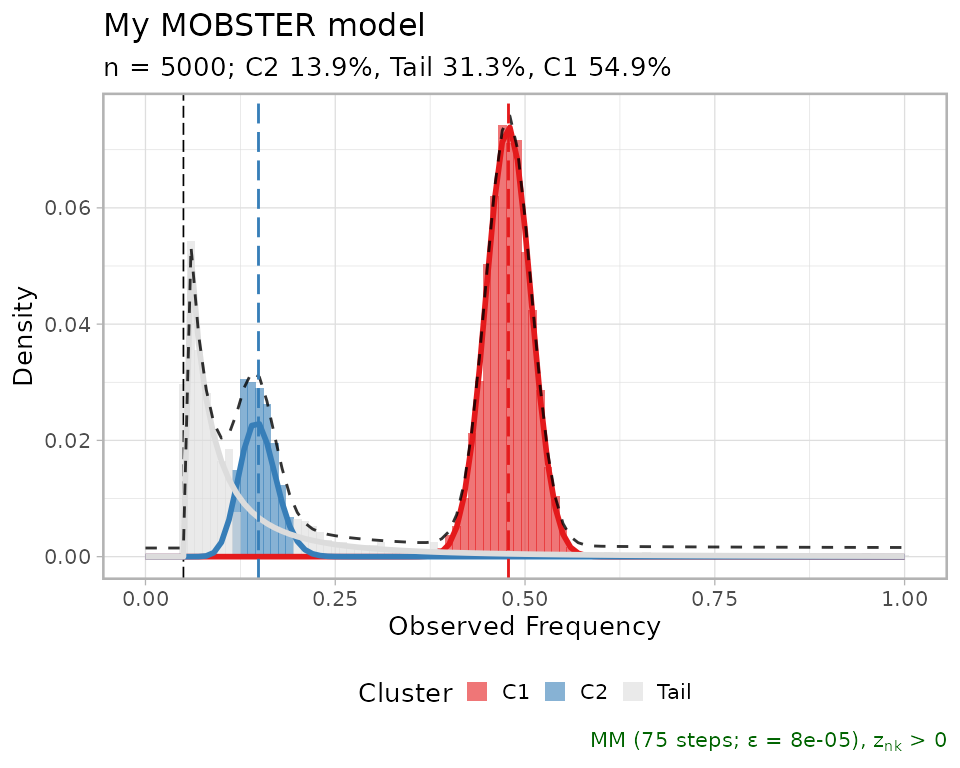

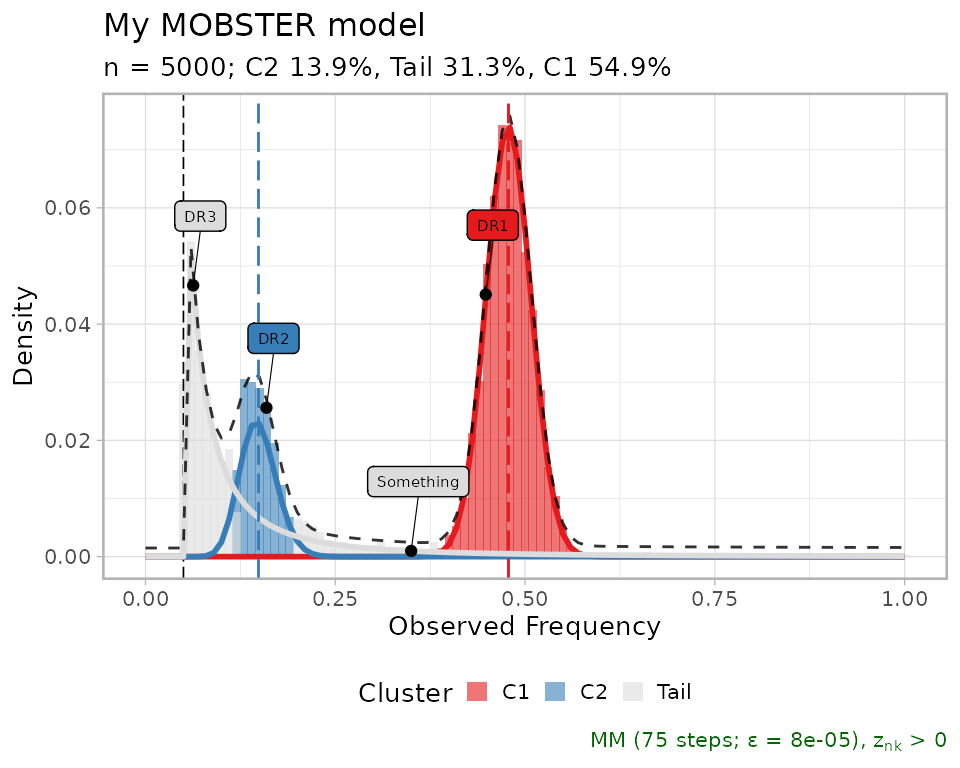
It is possible to annotate further labels to this plot, providing just a VAF value and a driver_label value. Each annotation points to the VAF value on the x-axis, and on the corresponding mixture density value for the y-axis.

plot(best_fit,
     annotation_extras = 
       data.frame(
         VAF = .35, 
         driver_label = "Something",
         stringsAsFactors = FALSE)
     )

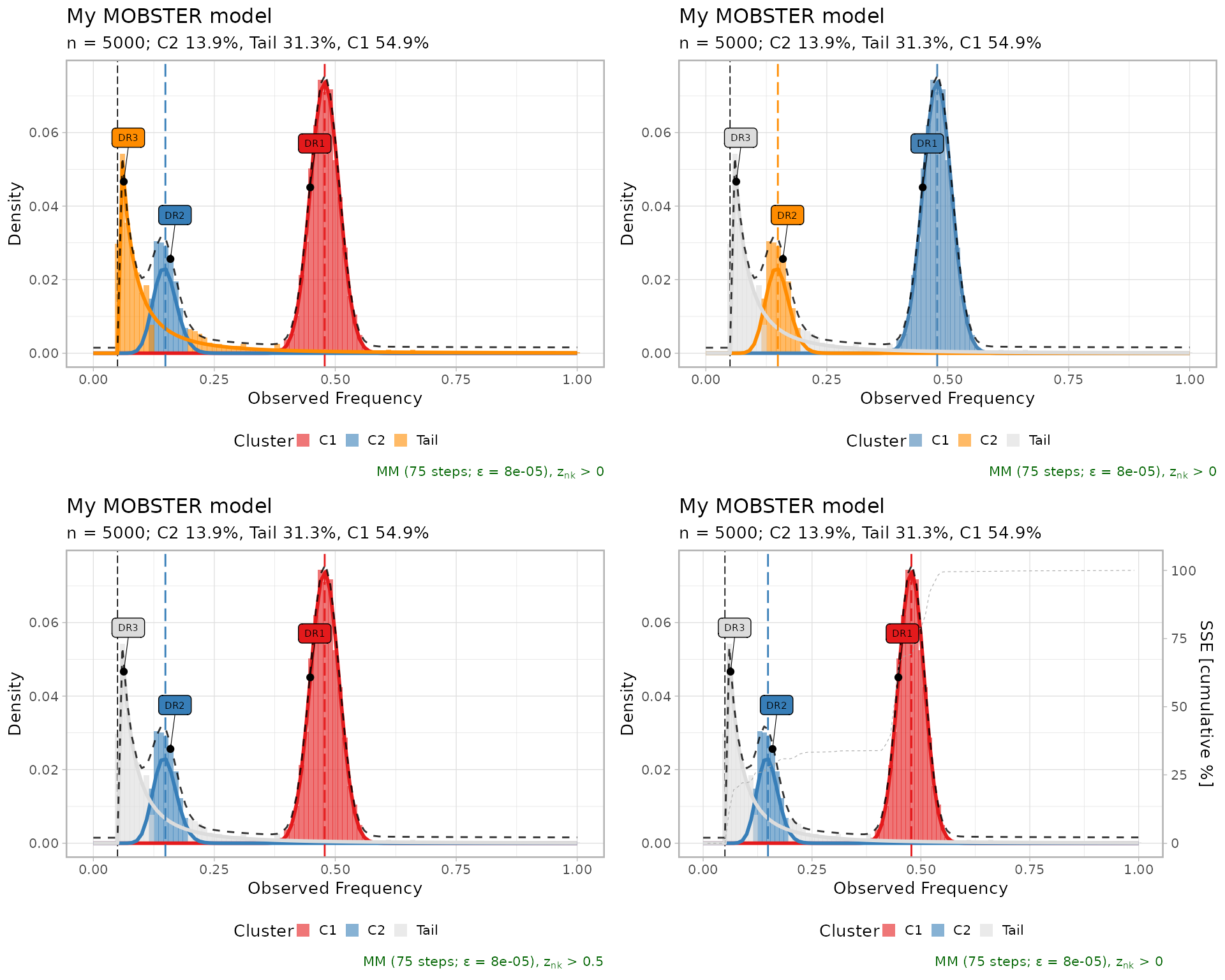
Other visualisations can be obtained as follows

ggpubr::ggarrange(
  plot(best_fit, tail_color = "darkorange"),                  # Tail color
  plot(best_fit, beta_colors = c("steelblue", "darkorange")), # Beta colors
  plot(best_fit, cutoff_assignment = .50),                    # Hide mutations based on latent variables 
  plot(best_fit, secondary_axis = "SSE"),               # Add a mirrored y-axis with the % of SSE
  ncol = 2,
  nrow = 2
)

Fit statistics

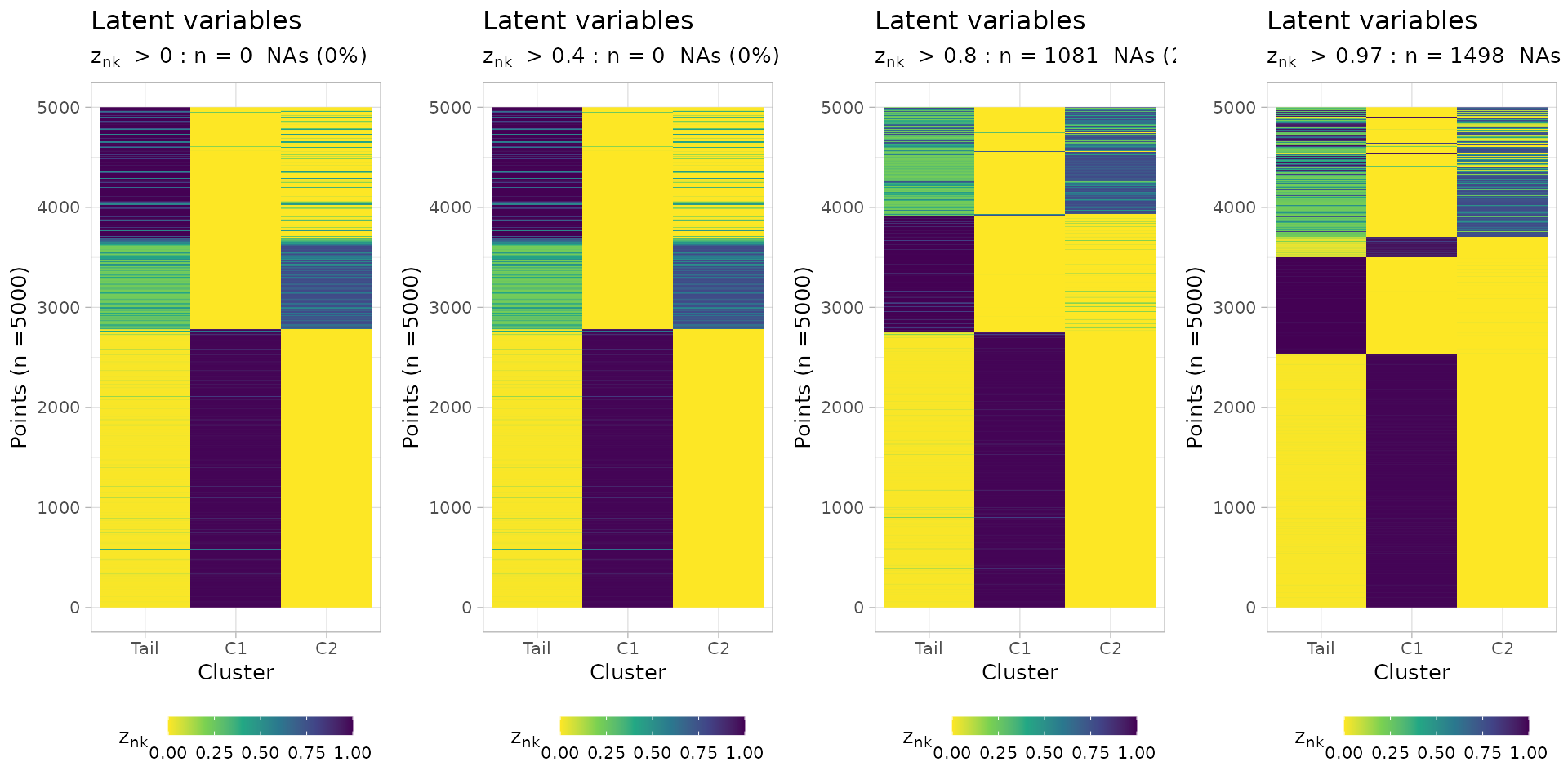
You can plot the latent variables, which are used to determine hard clustering assignments of the input mutations. A cutoff_assignment determines a cut to prioritize assignments above the hard clustering assignments probability. Non-assignable mutations (NA values) are on top of the heatmap.

ggpubr::ggarrange(
  mobster::plot_latent_variables(best_fit, cutoff_assignment = 0),
  mobster::plot_latent_variables(best_fit, cutoff_assignment = 0.4),
  mobster::plot_latent_variables(best_fit, cutoff_assignment = 0.8),
  mobster::plot_latent_variables(best_fit, cutoff_assignment = 0.97),
  ncol = 4,
  nrow = 1
)

You can plot a barplot of the mixing proportions, using the same colour scheme for the fit (here, default). The barplot annotates a dashed line by default at 2%.

plot_mixing_proportions(best_fit)
#> Warning in geom_text(data = NULL, aes(label = "2%", x = 0.1, y = 0.04), : All aesthetics have length 1, but the data has 2 rows.
#> ℹ Please consider using `annotate()` or provide this layer with data containing
#>   a single row.
#> Warning: No shared levels found between `names(values)` of the manual scale and the
#> data's colour values.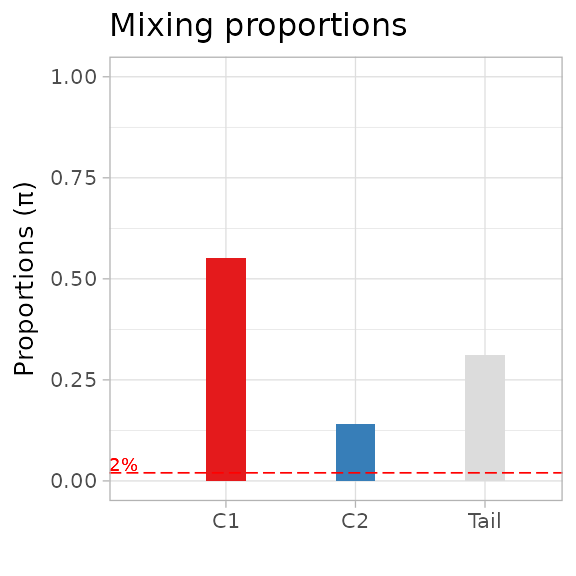

The negative log-likelihood NLL of the fit can be plot against the iteration steps, so to check that the trend is decreasing over time.

plot_NLL(best_fit)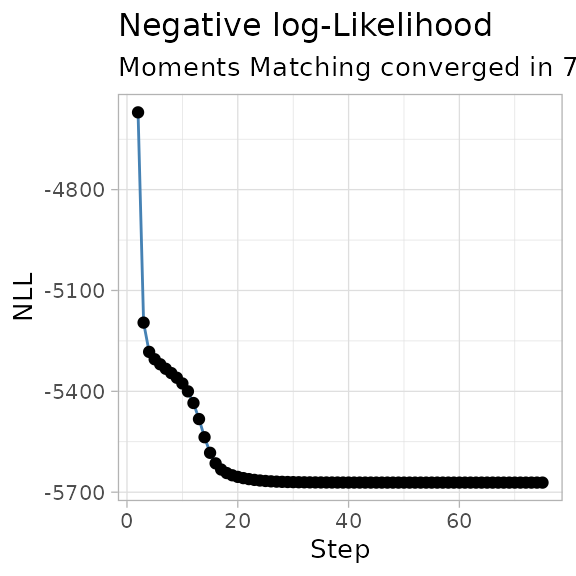

A contributor to the NLL is the entropy of the mixture, which can be visualized along with the reduced entropy, which is used by reICL.

plot_entropy(best_fit)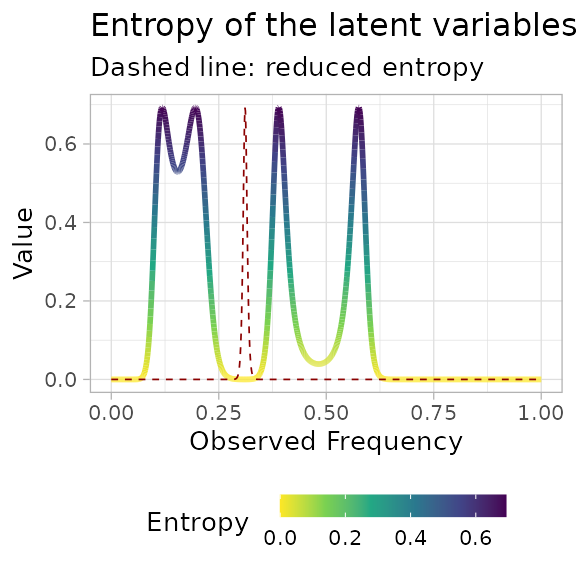

Inspecting alternative fits

Alternative models are returned by function mobster_fit, and can be easly visualized; the table reporting the scores is a good place to start investigating alternative fits to the data.

print(fit$fits.table)
#>         NLL        BIC        AIC   entropy        ICL reduced.entropy
#> 1 -5332.989 -10614.876 -10653.979  323.0129 -10291.863          0.0000
#> 5 -5301.274 -10551.444 -10590.547  375.9632 -10175.481          0.0000
#> 2 -5332.968 -10589.282 -10647.937 2179.1747  -8410.107       1894.6576
#> 4 -4442.905  -8834.707  -8873.810  544.0527  -8290.654        544.0527
#> 3 -1570.709  -3115.867  -3135.419    0.0000  -3115.867          0.0000
#>        reICL size K  tail
#> 1 -10614.876    6 1  TRUE
#> 5 -10551.444    6 1  TRUE
#> 2  -8694.625    9 2  TRUE
#> 4  -8290.654    6 2 FALSE
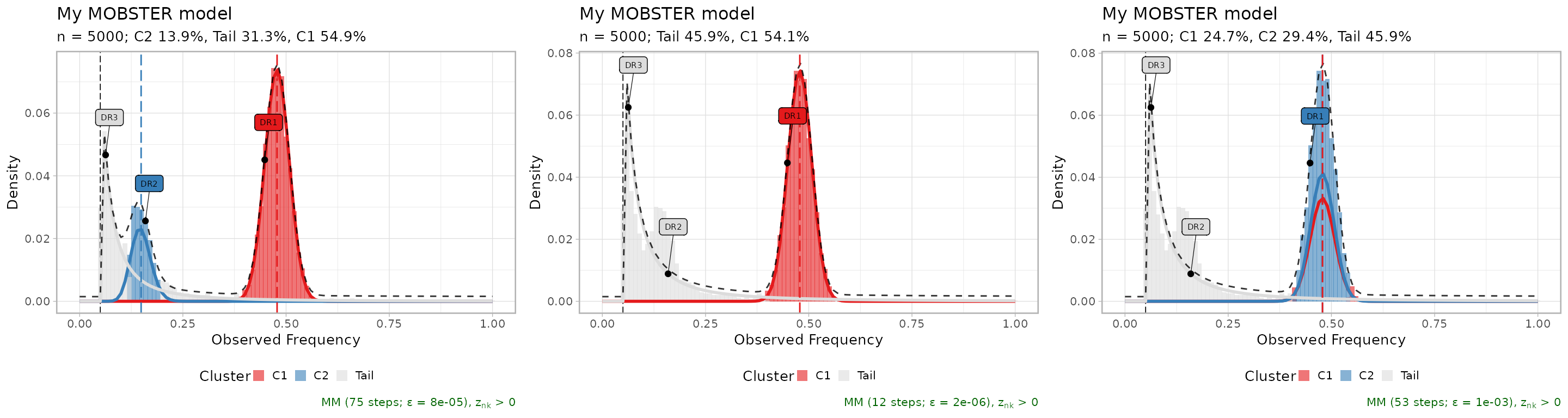
#> 3  -3115.867    3 1 FALSE

Top three fits, plot in-line.

ggpubr::ggarrange(
  plot(fit$runs[[1]]),
  plot(fit$runs[[2]]),
  plot(fit$runs[[3]]),
  ncol = 3, 
  nrow = 1
)

The sum of squared error (SSE) between the fit density and the data (binned with bins of size 0.01), can be plot to compare multiple fits. This measure is a sort of “goodness of fit” statistics.

# Goodness of fit (SSE), for the top 3 fits.
plot_gofit(fit, TOP = 3)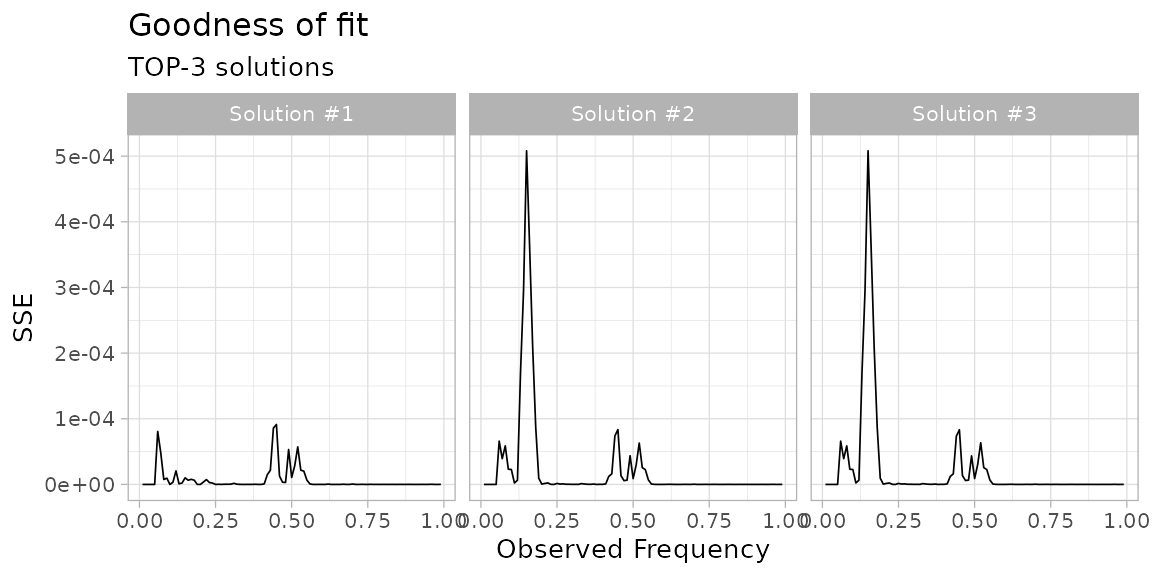

The scores for model selection can also be compared graphically.

plot_fit_scores(fit)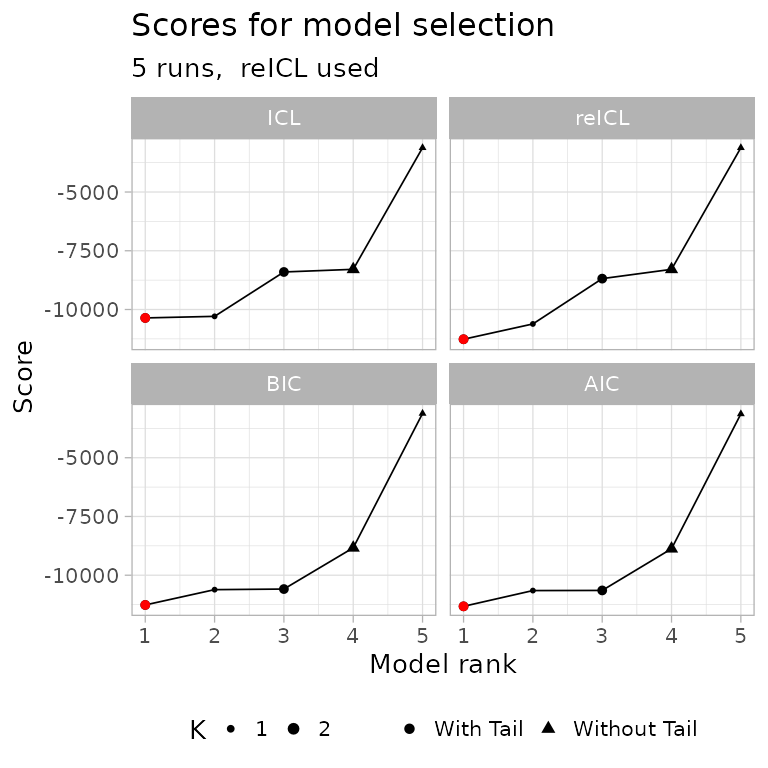

In the above plot, all the computed scoring functions (BIC, AIC, ICL and reICL) are shown. This plot can be used to quickly grasp the best model with, for instance, the default score (reICL) is also the best for other scores. In this graphics the red dot represents the best model according to each possible score.

Model-selection report

A general model-selection report assembles most of the above graphics.

plot_model_selection(fit, TOP = 5)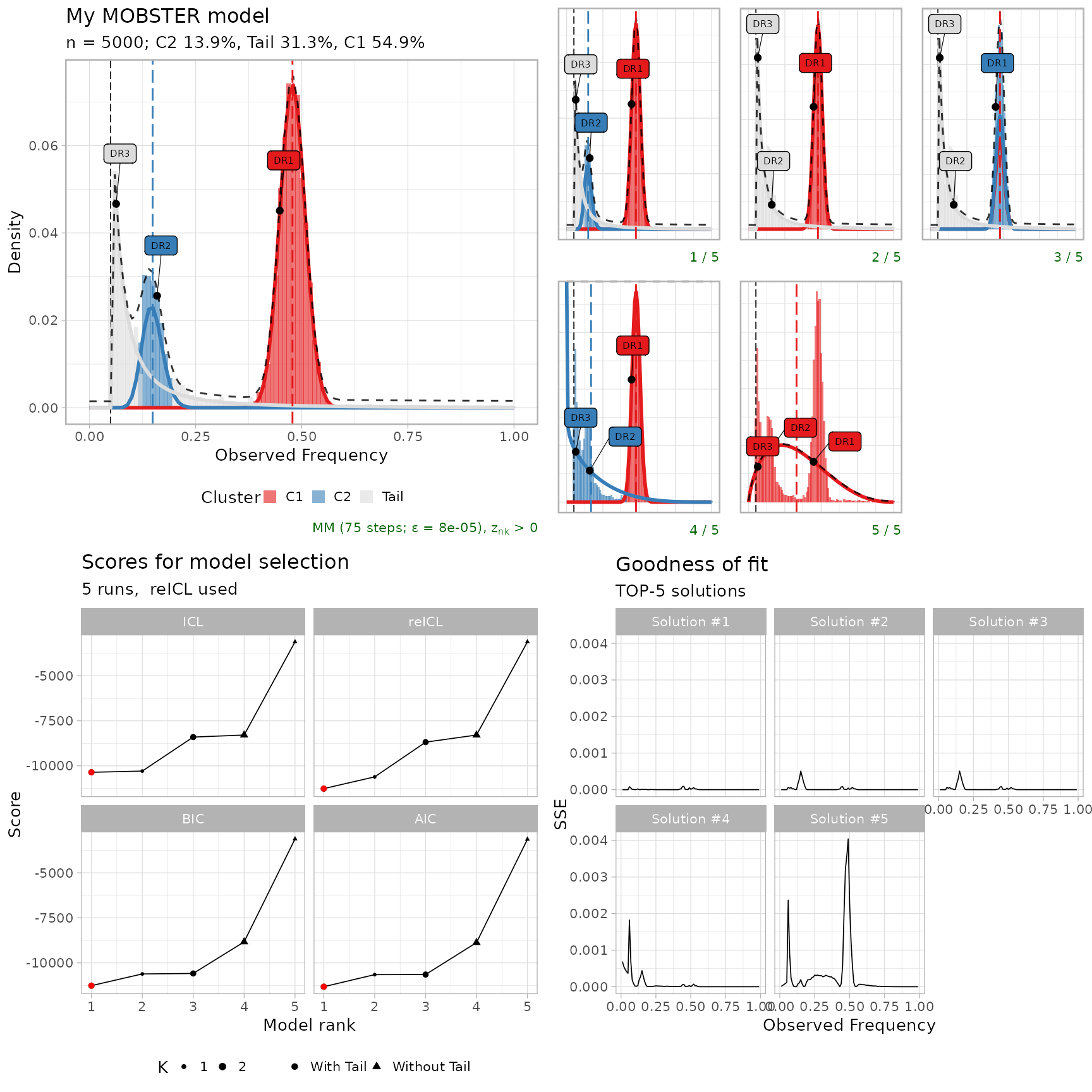

Fit animation

It seems useless, but if you want you can animate mobster fits using plotly.

example_data$is_driver = FALSE

# Get a custom model using trace = TRUE
animation_model = mobster_fit(
  example_data, 
  parallel =  FALSE, 
  samples = 3,
  init = 'random',
  trace = TRUE,
  K = 2,
  tail = TRUE)$best
#>  [ MOBSTER fit ] 
#> 

# Prepare trace, and retain every 5% of the fitting steps
trace = split(animation_model$trace, f = animation_model$trace$step)
steps = seq(1, length(trace), round(0.05 * length(trace)))
  
# Compute a density per step, using the template_density internal function
trace_points = lapply(steps, function(w, x) {
  new.x = x
  new.x$Clusters = trace[[w]]
  
  # Hidden function (:::)
  points = mobster:::template_density(
    new.x,
    x.axis = seq(0, 1, 0.01),
    binwidth = 0.01,
    reduce = TRUE
  )
  points$step = w
  
  points
},
x = animation_model)
  
trace_points = Reduce(rbind, trace_points)
  
# Use plotly to create a ShinyApp
require(plotly)
    
trace_points %>%
  plot_ly(
    x = ~ x,
    y = ~ y,
    frame = ~ step,
    color = ~ cluster,
    type = 'scatter',
    mode = 'markers',
    showlegend = TRUE
  )

Giulio Caravagna

21 November, 2025

Model plots

Fit statistics

Inspecting alternative fits

Model-selection report

Fit animation