5. Understanding Timing of Multiple Clonal Peaks

This vignette delves into how the tickTack package obtains timing results for clonal peaks using the fit_h function. It explains the underlying processes, including the computation of clonal peaks and the Stan model used for inference.

Key Components of the Analysis

This function performs hierarchical Bayesian inference using ADVI to approximate the posterior distributions of clock parameters for copy number alterations (CNAs). It iteratively fits models with different numbers of components (up to k_max), computes posterior summaries, and logs ELBO (Evidence Lower Bound) values for each fit.

The input data are: - x list: A CNAqc object containing mutation and CNA data. - max_attempts num: Maximum number of repeated inference attempts for ADVI. - INIT logical: Whether to perform initialization of parameters. - tolerance num: Tolerance level for ELBO optimization. - possible_k chr: Possible karyotype configurations (e.g., "2:1", "2:2", "2:0"). - alpha num: Confidence interval level for binomial filtering. - min_mutations_number num: Minimum number of mutations required for a segment to be included in inference. - n_components num: Number of components specified by the user (overrides automatic determination).

It returns a list containing processed input data, posterior draws, ELBO iterations, and other inference results.

Steps of the `fit_h` Function

Step 1: Validate Input Data

Extract mutation and CNA data from the CNAqc object.
Ensure both mutations and CNA data are non-empty. If empty, the function terminates with an error.

Step 2: Prepare Input Data

Use prepare_input_data to filter and format mutation and CNA data based on the provided karyotypes (possible_k), confidence intervals (alpha), and minimum mutations per segment (min_mutations_number).
Extract accepted_cna and input_data for inference.

Step 3: Determine Maximum Number of Components (`k_max`)

If n_components is not provided, calculate k_max based on the number of segments (S) using predefined rules.

Step 4: Iterative Inference for Each Component Count (`K`)

For each K from 1 to k_max: - Add K to the input_data. - If INIT is enabled, initialize parameters using get_initialization. - Fit the model using fit_variational_h with ADVI. - Extract relevant posterior variables (tau and w) and compute summaries. - Compute clock assignments for segments using compute_clock_assignment. - Store results, including posterior summaries and clock assignments.

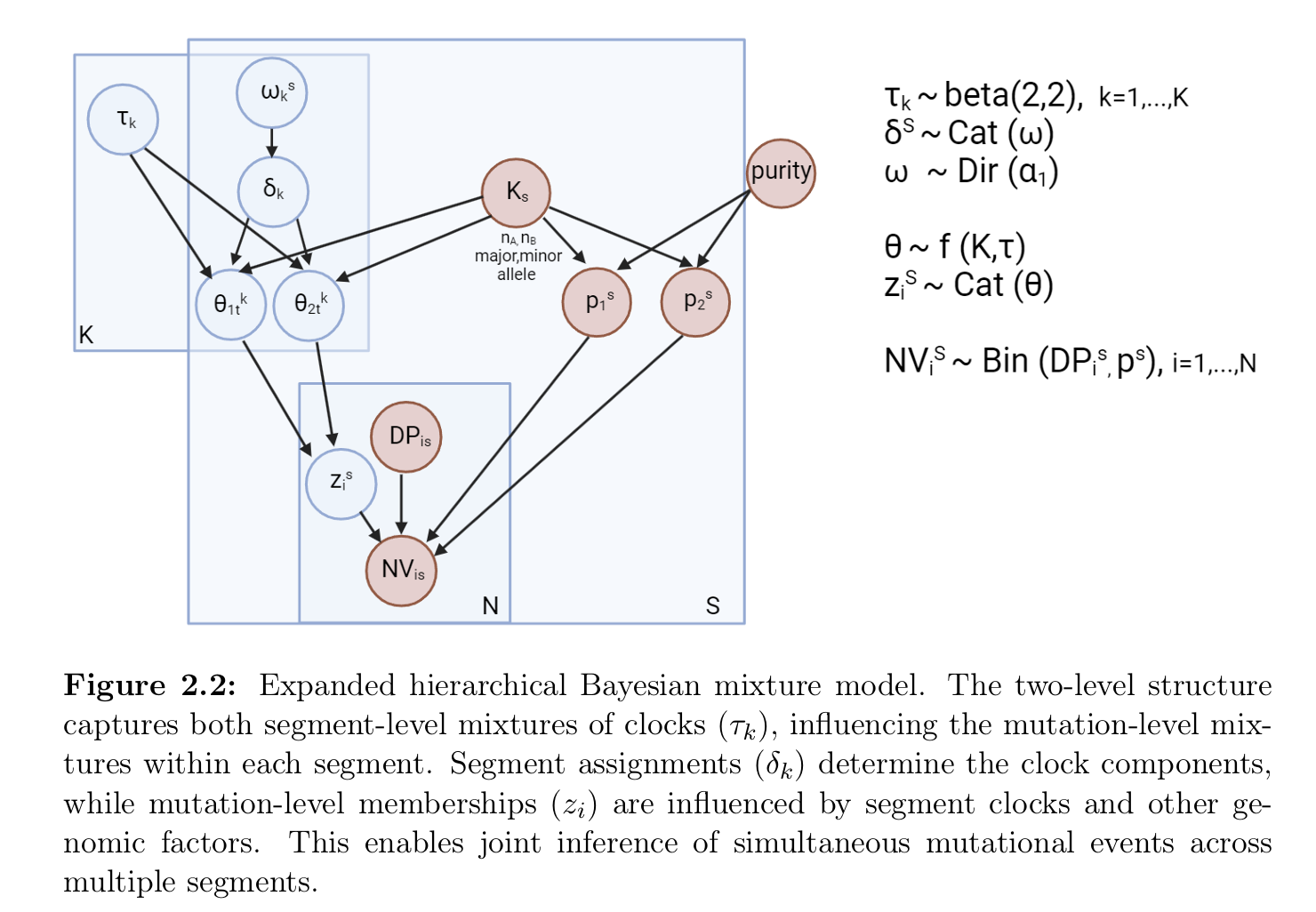
The model to fit is described by the following probabilistic graphical model. Overview timing problem

The model estimates the posterior distribution of tau and weights , which represents the timing of clonal expansions.

The stan code used for the model is divided in the following pieces.

Data block

data {
  // input the karyotyoe to specify the formula for theta

  int S;                        // number of segments
  int K;                        // clocks
  int N;                        // total number of mutations
  array[S] int karyotype;       // list of karyotype associated wit the segments
  array[N] int seg_assignment;  // segment_id assignment to the mutations
  array[S,2] real peaks;        //for each segment, S vectors of dim 2
  array[N] int NV;              // for all the segments
  array[N] int DP;
}

Parameters block

parameters {
  array[S] simplex[K] w;              // simplex[K] w[N] mixing proportions for each segment group; check prior should be more on the higher values
  vector<lower=0.0001,upper=0.999>[K] tau;     //clocks   ordered[K] tau  vector<lower=0,upper=1>[K]
  //vector[K] alpha;
  simplex[K] phi;
  real<lower=0> kappa;
}

Transformed parameters block

transformed parameters{

  array[S] vector[K] perturbed_w;  // Pesi perturbati e rinormalizzati
  real<lower=0> epsilon;
  epsilon = 0.01;
  for (s in 1:S) {
    for (k in 1:K) {
      if (w[s][k] > 0.5) {
        perturbed_w[s][k] = w[s][k] - epsilon;
      } else {
        perturbed_w[s][k] = w[s][k] + epsilon;
      }
    }
    // Rinormalizza i pesi
    perturbed_w[s] = perturbed_w[s] / sum(perturbed_w[s]);
  }

  array[S,K,2] real<lower=0,upper=1> theta; //binomial mixing proportions // array[S,K] simplex[2] theta;

  for (s in 1:S){
   for (k in 1:K){
      if (karyotype[s] == 1) {
        theta[s,k,1] = (3 - 2*tau[k]) / (3 - tau[k]);      // 2:1
        theta[s,k,2] = tau[k] / (3 - tau[k]);
      }
      else {
        theta[s,k,1] = (2 - 2*tau[k]) / (2 - tau[k]);      // 2:0 - 2:2
        theta[s,k,2] = tau[k]/(2 - tau[k]);
      }
    }
  }

  vector[K] alpha = kappa * phi;
}

Model block

model {
  vector[K*2] contributions;              //real contributions[K * 2];  // Array to hold contributions for log_sum_exp

  // priors
  phi ~ dirichlet(rep_vector(1.0, K));;
  kappa ~ gamma(2, 0.5);                  // strictly positive with a long right tail.
                                          // phi = expected value of w, kappa (minus K) = concentrazione della distribuzione / strength of the prior mean measured in number of prior observations.

  for (s in 1:S){
      w[s] ~ dirichlet(alpha);
  }

  for (k in 1:K) {
    tau[k] ~ beta(2,2);                   // Beta prior for tau
  }
  

  //likelihood
    for (i in 1:N) {
    int c = 1;
    
    for (k in 1:K) {
      for (j in 1:2) {
        
        real contribution = log(perturbed_w[seg_assignment[i], k]) +
                            log(theta[seg_assignment[i], k, j]) +
                            binomial_lpmf(NV[i] | DP[i], peaks[seg_assignment[i], j]);

        contributions[c] = contribution;
        c += 1;
      }
    }
    target += log_sum_exp(contributions);
  }

}

The model block contains three components:

Prior: The line tau[k] ~ beta(2,2) applies a Beta prior to the components’ values. The line w[s] ~ dirichlet(alpha); applies a Dirichlet prior to the mixture probabilities that depends on alpha = phi * kappa. This means that we do not a priori favor one clock component over the other unless there is data evidence. The lines phi ~ dirichlet(rep_vector(1.0, K)); and kappa ~ gamma(2, 0.5); apply the priors to the reparametrization values for the alpha parameter of the weights.
Likelihood: The likelihood is computed using the binomial_lpmf(NV[i] | DP[i], peaks[seg_assignment[i], j]) (or the Negative binomial). This term computes the probability of observing NV[i] variant reads given sequencing depth DP[i] and a given theoretical clonal peak value peaks[k].
Marginalization: The line log_sum_exp(contributions) computes the log marginal likelihood by summing over possible contributions (karyotypes) using the softmax approach, allowing the model to integrate over possible karyotype contributions (omega).

Generated quantities

generated quantities {
  
  //array[N] vector[K*2] log_lik_matrix;
  
  vector[N] log_lik;                        // log-likelihood for each data point
  for (i in 1:N) {
    vector[K*2] contributions;
    int c = 1;
    for (k in 1:K) {
      for (j in 1:2) {
        contributions[c] = log(w[seg_assignment[i],k]) + log(theta[seg_assignment[i],k,j]) + binomial_lpmf(NV[i] | DP[i], peaks[seg_assignment[i],j]);
        c += 1;
      }
    }
    log_lik[i] = log_sum_exp(contributions);
    //log_lik_matrix[i] = contributions;
  }

}

Step 5: Log ELBO Iterations

Extract ELBO values from the output files of the model fit and save them for each K.

Step 6: Compile Results

Store posterior draws, summaries, log-likelihood contributions, and ELBO iterations in lists for each K.
Return the compiled results as a list:
- data: Processed input data.
- draws_and_summary: Posterior draws and summaries for each K.
- log_lik_matrix_list: Log-likelihood matrices for each K.
- elbo_iterations: ELBO iteration data for each K.

Step 7: Update CNAqc Object

Add the results to the CNAqc object as results_timing.